动态规划(5)—算法导论(20)

2016年06月12日 15:04

1. 提出问题

假设我们要设计一个将英语翻译成法语的程序，即对英文文本中出现的每个单词，我们需要查找其对应的法语单词。为了实现这一查找操作，我们可以构建一棵二叉搜索树，将n个英文单词作为关键字，对应的法语单词作为关联数据。

通过使用红黑树或其他平衡搜索树结构，我们可以做到平均搜索时间为$O(lgn)$。但需要注意到的是，每个单词的出现频率是不一样的，并且这种频率的差异还是比较大的。比如像 "the" 这种单词，出现的频率就比较高，而像 "machicolation" 这类单词几乎就不会出现。因此，如果我们在不考虑单词出现频率的情况下去构造二叉搜索树，很有可能将类似 "the" 这类高频单词置于树的较深的结点处，这样势必会使搜索时间增加。

于是，在给定单词出现频率的前提下，我们应该如何去组织一棵二叉搜索树，使得所有搜索操作访问的结点总数最少呢？这便是**二叉搜索树问题(optimal binary search tree)**。其形式化的描述如下：

给定一个包含n个不同关键字且已排序的序列$K = < k_1, k_2,...,k_n >$(其中$k_1<k_2<...<k_n$)和关键字$k_i$的搜索频率$p_i,i=1,2...n$；还给定$(n+1)$个“伪关键字”$d_0,d_1,...d_n$，表示不在K中的值（因为有些搜索值可能不在K中），同时也给出其被搜索的频率$q_i$。要用这些关键字构造一棵二叉搜索树T使得在T中搜索一次的期望搜索代价最小。

期望搜索代价E(T)可由如下公式计算出：

$$E(T) = \sum_{i=1}^n(depth(k_i)+1)\cdot p_i+\sum_{i=0}^n(depth(d_i)+1)\cdot q_i$$

其中，depth(node)表示node的深度（约定根结点的深度为0）。

由于

$$\sum_{i=1}^np_i + \sum_{i=0}^nq_i = 1$$

我们可以将上述E(T)计算式变形为：

$$E(T) = 1 + \sum_{i=1}^ndepth(k_i) \cdot p_i + \sum_{i=0}^n depth(d_i) \cdot q_i$$

举个例子，对一个n = 5的关键字集合，给出如下搜索概率：

我们可以这么构造出一棵二叉搜索树：

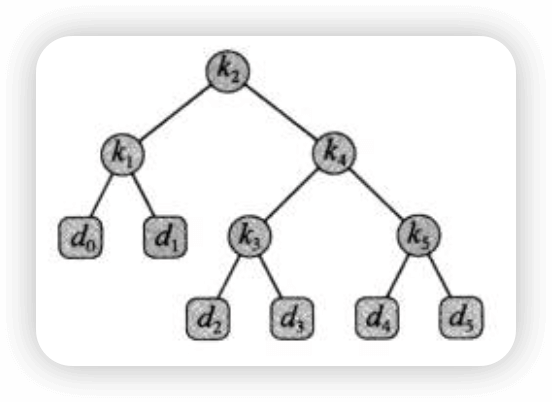
也可以这么构造：

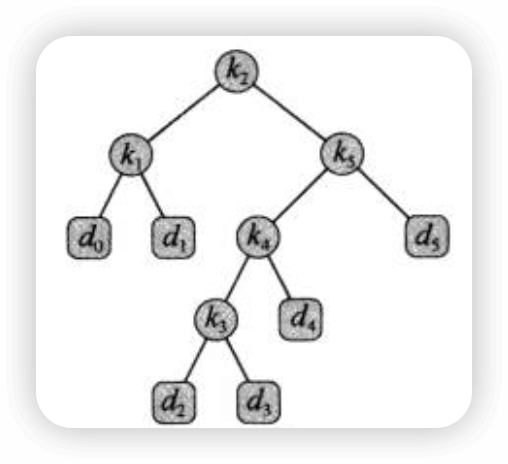
通过计算可以发现，第一种方式的搜索代价为2.8，而第二种方式的搜索代价为2.75，因此第二种方式更好。事实上，第二种方式构造的二叉搜索树是一棵最优搜索二叉树。从该例子中我们可以看出，最优二叉搜索树不一定是高度最矮的二叉树，而且概率最大的关键字也不一定出现在根结点，不要把它和哈夫曼树混淆。

PS：当然，上述采用二叉搜索树的策略也许并不是最好的，比如可以采用效率更高的hashtable，比如采用分块查找。但是，二叉搜索树较hashtable而言，也有其优势，具体可参见 Advantages of BST over Hash Table。这里只是以这个案例引出最优二叉搜索树问题。

2. 分析问题

同样，我们试图用动态规划方法来解决该问题。和之前一样，先考察动态规划方法的两个重要特性。

2.1 最优子结构

假定一棵最优二叉搜索树T有一棵子树T'，那么如果将T'单独拿出来考虑，它必然也是一棵最优二叉搜索树。我们同样可以用剪切-粘贴法来证明这点：如果T'不是一棵最优二叉搜索树，那么我们把有T'包含的关键字组成的最优二叉搜索树”粘贴“到T'位置，此时构造的树一定比之前二叉搜索树T更优，这与T是最优二叉搜索树像矛盾，以上得证。

上述证明了该问题具有最优子结构性质，接着我们考虑如何通过子问题的最优解来构造原问题的最优解。一般地，给定关键字序列 $k_i,...,k_j$，$1 \leqslant i \leqslant j \leqslant n$，其叶结点必然是伪关键字$d_{i-1}...d_j$。假定关键字$k_r(i \leqslant r \leqslant j)$是这些关键字的最优子树的根结点，那么$k_r$的左子树包含关键字$k_1, k_2...k_{r-1}$，其右子树包含关键字$k_{r+1}...k_j$。只要我们检查所有可能的根结点$k_r$，并对其左右子树分别求解，即可保证找出原问题的最优解。

2.2 子问题重叠

从以上分析中我们发现，求解$k_r$的左右子树问题和求解原问题的模式是一样的，因此我们可以用一个递归式来描述原问题的解。

定义$e(i, j)$(其中$i\geqslant 1,j \leqslant n$ 且$j \leqslant i-1)$为在包含关键字$k_i...k_j$的最优二叉搜索树中进行一次搜索的期望代价；$w(i, j)$表示如下包含关键字$k_i,...,k_j$的子树的所有元素概率之和：

$$w(i, j) = \sum_{k=i}^j p_k + \sum_{k=i}^j q_k$$

当一棵树成为一个结点的子树时，其上的每一个结点的深度都会增加1。根据之前的期望搜索代价$E(T)$的计算公式的变形式

$$E(T) = 1 + \sum_{i=1}^ndepth(k_i) \cdot p_i + \sum_{i=0}^n depth(d_i) \cdot q_i$$

我们可以得出，**当包含关键字$k_i...k_j$的最优二叉搜索树中的每个结点的深度增加1时，$E(T)$将增加$w(i, j)$**。于是我们可得到如下公式：

$$e(i, j) = p_r + [e(i, r-1) + w(i, r-1)] + [e(r+1, j) + w(r+1, j)]$$

注意到：

$$w(i, j) = w(i, r-1) + p_r +w(r+1, j)$$

于是上述$e(i, j)$递推式可简化为：

$$e(i, j) = e(i, r-1) + e(r+1, j) + w(i, j)$$

需要注意的是，我们在上面定义$e(i, j)$时，给出了$i$ 与 $j$的取值范围。其中有种特别的情况是，当$j=i-1$时，表示只包含“伪关键字”结点$d_{r-1}$，此时搜索期望代价$e(i, i-1) = q_{i-1}$

根据以上分析，我们可得最终的递推式：

$$e(i, j) = \begin{cases} q_{i-1} & \text{ 若$j = i-1$}\\ \min \limits_{i\leqslant r \leqslant j}[e(i, r-1)+ e(r+1, j) + w(i, j)] & \text { 若$i\leqslant j$} \end{cases}$$

我们的最终目标是计算出$e(1, n)$。

同矩阵链的乘法问题一样，该问题的子问题是由连续的下标子域构成，许多子问题“共享”另一些子问题，即子问题重叠。

3. 解决问题

有了前两部分的分析，我们可以很容易地设计出一个自底向上的动态规划算法来解决该问题。

下面给出Python的实现版本：

# 计算e与root

# e[i][j]意思与上述分析中的e(i, j)一致;
# root[i][j]表示包含关键字k_i...k_j的最优二叉搜索树的根结点关键字的下标;
# w[i][j]意思也与上述分析中的w(i, j)一致，这里用w数组作为“备忘录”,
# 用公式 w[i][j] = w[i][j - 1] + p[j] + q[j]来计算w[i][j]，可利用上之前计算出的w[i][j - 1],
# 这样可以节省Θ(j - i)次加法。
def optimal_bst(p, q, n):
    e = [[0 for i in range(n + 1)] for j in range(n + 2)]
    w = [[0 for i in range(n + 1)] for j in range(n + 2)]
    root = [[0 for i in range(n + 1)] for j in range(n + 1)]
    for i in range(1, n + 2):
        e[i][i - 1] = q[i - 1]
        w[i][i - 1] = q[i - 1]
    for l in range(1, n + 1):
        for i in range(1, n - l + 2):
            j = i + l - 1
            e[i][j] = float('inf')
            w[i][j] = w[i][j - 1] + p[j] + q[j]
            for r in range(i, j + 1):
                t = e[i][r - 1] + e[r + 1][j] + w[i][j]
                if t < e[i][j]:
                    e[i][j] = t
                    root[i][j] = r
    return e, root

# 先序遍历打印树
def printByPreorderingTraverse(root, i, j):
    if i > j:
        return
    r = root[i][j]
    print(r, end='')
    if r > 0 :
        printByPreorderingTraverse(root, i, r - 1)
    if r < len(root) - 1:
        printByPreorderingTraverse(root, r + 1, j)

if __name__ == '__main__':
    p = [0, 0.15, 0.10, 0.05, 0.10, 0.20] 
    q = [0.05, 0.10, 0.05, 0.05, 0.05, 0.10]
    n = 5
    e, root = optimal_bst(p, q, n)
    print('最优期望搜索代价为：', e[1][n])
    print('最优搜索二叉树的先序遍历结果为：', end='')
    printByPreorderingTraverse(root, 1, n)

打印结果为：

最优期望搜索代价为： 2.75
最优搜索二叉树的先序遍历结果为：21543