二叉搜索树—算法导论(14)

1. 什么是二叉搜索树

顾名思义，二叉搜索树是以一棵二叉树来组织的。如下图，这样的一棵树可以使用一个链表数据结构来表示，其中的每一个节点是一个对象。除了key和卫星数据之外，每个节点还包含属性left（左孩子）、right（右孩子）、和p（双亲）（若不存在，则值为NILL）。

二叉搜索树 中的关键字总是以满足二叉搜索树性质的方式存储：

设x是二叉搜索树的一个节点。如果y是x左子树中的一个节点，那么y.key≤x.key。如果y是x右子树中的一个节点，那么y.key≥x.key。

二叉搜索树性质允许我们使用一种简单的递归算法来按一定的顺序输出二叉搜索树中的所有关键字。我们常用的有先序遍历（输出的子树根的关键字位置位于左子树关键字和右子树关键字之间）、中序遍历、后序遍历。

下面给出先序遍历的递归算法：

我们可以证明：遍历一棵有n个节点的二叉搜索树需要花费θ(n)的时间（证明略）。

2. 查询二叉搜索树

这一小节，我们来讨论二叉搜索树的诸如：SEARCH，MINIMUM，MAXIMUN，SUCCESSOR，PERDECESSOR操作。

search

我们使用如下一种算法去查询一棵二叉搜索树。该方法要求输入一个指向根节点的指针x和待查找的关键字k；输出为指向关键字为k的节点的指针（若存在。否则输出NIL）。

我们很容易知道，该查询算法的时间为O(h)，其中h为树的高度。

更好地，我们可以用如下迭代来替代递归，因为递归可能会造成栈内存溢出，在大多数计算机上，迭代版本的效率要更高。

minimum和maximum

由于二叉搜索树性质的存在，我们可以很容易的找出树中的最大和最小关键字元素。

同样，上面的两种方法均可以在O(h)时间内完成。

successor和predecessor

给定一棵二叉搜索树的某个节点，有时我们需要按中序遍历的次序去查找该节点的前驱和后驱。如在下图中，我们容易看出，key为4的节点的前驱是key为3的节点，后驱是key为6的节点；key为7的节点的前驱是key为6的节点，后驱是key为9的节点。

下面是求某节点后驱的算法：

解释一下上面求后驱的过程。我们分两种情况讨论：

如果x的右子树不为NIL，那么x的后继即为右子树中key最小的元素。
如果x的右子树为NIL，那么x的后继节点必将在其祖先节点（包括父节点）中产生。并且该祖先节点必须是从下至上，第一次满足自己为自己父节点的右节点。

同理，我们可以求出x的前驱节点，这里就不给出算法了。

很容易看出，它们所需的时间均为O(h)。

由此，我们得出：在一棵高度为h的二叉搜索树上，集合操作SEARCH，MINIMUM，MAXIMUN，SUCCESSOR，PERDECESSOR都可以在O(h)时间内完成。

3. 插入和删除

插入

相比删除操作，插入操作相对简单一些。下面给出insert算法。该算法的作用是，将一个新节点z插入到一棵二叉搜索树T中。

算法很简单，这里就不做说明了。

同样可以看出，插入操作的时间为O(h)。

删除

我们按照被删除的节点的子节点个数，分以下三种情况来讨论：

被删除节点没有孩子。只需要修改其父节点，用NIL去替换自己。
被删除节点有一个孩子。也只需要修改其父节点，用这个孩子去替换自己。
被删除节点有两个孩子。那么先找z的后继y（一定在z的右子树中），并让y占据树中z的位置。z的原来的右子树部分称为y的新的右子树，并且z的左子树成为y的左子树。

前两种情况比较简单，至于第三种情况，我们还可以细分：

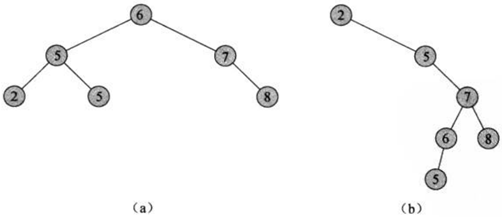
如果z的后继y就是z的右孩子（即y没有左孩子），直接用y代替z，并保留y的右子树，如下图所示：
如果z的后继y不是z的右孩子，先用y的右孩子替换y，再用y替换z。如下图所示：

为了实现上面的过程，我们先来实现transplant过程。该过程能够实现让子树v代替子树μ。实现算法如下：

利用transplant，我们根据上述的讨论来实现删除操作：

注意到上述删除操作过程并没有给出我们上述讨论中，情况①中z没有孩子的情况。事实上，上述讨论中情况1已经被包含在情况2中，即z没有孩子的情况等价于z有一个key为NIL的左孩子或有一个key为NIL的右孩子。

分析该算法，我们发现除了transplant外，其他操作均花费常量时间。因此删除操作将花费O(h)时间。

综合以上的所有分析，我们可知：二叉搜索树上的每个基本操作都可以在O(h)时间内完成（其中h为树的高度）。

4. 随机构建二叉搜索树

我们先给出随机构建二叉搜索树的定义：向一棵空树随机的插入n个关键字而得到的树。这里随机的意思是n个关键字的n!种排列都等可能的出现。

我们要证明如下定理：

一棵有n个不同关键字的随机构建二叉搜索树的期望高度为O(lgn)。

先定义三个随机变量Xn，Yn，Rn，其中，Xn表示一棵有n个不同关键字的随机构建二叉搜索树的高度；Yn=2^Xn表示二叉搜索树的指数高度（exponential height）。Rn表示当在n个不同的关键字中选择一个作为树根时，该关键字在这n个关键字集合中的秩（rank）（即Rn表示这些关键字排好序后这个关键字应占据的位置）。这样如果Rn = i，那么表示根的左子树有i-1个元素，右子树有n-i个元素，此时有：

Y_n = 2 · max(Y_i-1, Y_n-i)

我们再定义一个指示器随机变量Z_n,i，Z_n,i = I{R_n = i}。因为R_n对于集合｛1，2，…，n｝中的任一元素都是等可能的，因此有：

p(R_n = i) = 1 / n,(i=1,2,..., n)\\ E(Z_n,i) = 1 / n

由于Z_n,i只等于1或0，且

Y_n = 2 · \max(Y_{i-1}, Y_{n-i})=\sum_{i=1}^nZ_{n,i}(2\cdot\max(Y_{i-1}Y_{n-i}))

于是有：

\begin{align} E[Y_n] &= E[\sum _{i=1} ^ n Z_{n,i}(2 * max(Y_{i-1}, Y_{n-i})] \\ &= \sum_{i=1}^n E[Z_{n,i}(2 * max(Y_{i-1}, Y_{n-i}))] \\ &= \sum_{i=1}^n E[Z_{n,i}]E[2*max(Y_{i-1}, Y_{n-i})] \\ &= \sum_{i=1}^n \frac 1 n * E[2 * max(Y_{i-1}, Y_{n-i})] \\ &= \frac 2 n \sum_{i=1}^nE[max(Y_{i-1}, Y_{n-i})] \\ &\leq \frac 2 n \sum_{i=1}^n (E[Y_{i-1}] + E[Y_{n-i}]) \end{align}

在上式最后的和式中， $Y[0],Y[1],...,Y[n-1]$ 都会出现两次（ $E[Y_{i-1}]$ 和 $E[Y_{n-i}]$ 都会出现），因此：

E[Y_n] \leq \frac{4}{n}\sum_{i=0}^{n-1}E(Y_i)

上式是一个递归式，我们可以猜测：

E(Y_n) \leq \frac{1}{4}C_{n+3}^3

并用数学归纳法可证明（这里略）。

由Jensen不等式，我们可得进一步可得：

2^{E[X_n]} \leq E[2^{x_n}]=E[Y_n]

于是，

2^{E[X_n]} \leq \frac{1}{4}(^{n+3}_3)=\frac{1}{4}\cdot\frac{(n+3)(n+2)(n+1)}{6}=\frac{n^3+6n^2+11n+6}{24}

两边取对数，最终得：

E[x_n]=O(\lg n)

二叉搜索树—算法导论(14) 2015年10月10日 20:10